





We have underlined the main causes of ambiguity, but many others exists. Now I want to talk about the technique called of disambiguation. Disambiguation is used in order to solve these ambiguities in an automatic way. (For automatic I refer to techniques that can be translate in a programming language and therefore useful in order to construct an intelligent agent). We begin just from the creation of a " Model of the World ", to which we have already pointed out dealing of the ambiguities of semantic type.
Model of the World.
It is based on the possibility that a fact happens. A model of
the world correctly developed would solve many semantic ambiguity
like the one we talked about with the sentence "the car hit the pole while it is moving.".
But how a model of the world is constructed? We can
start by defining objects or classes from which we will
derive other objects adding to each new class some more property that characterize it
(are you familiar with the concept of heredity of
modern programming languages?).
So we define the object Entity. From the object Entity we
derive the objects Animal, Vegetable, Mineral.
Continue the derivations like in figure, remembering that
every derived object inherits all the property of the object from
which it has been derived.
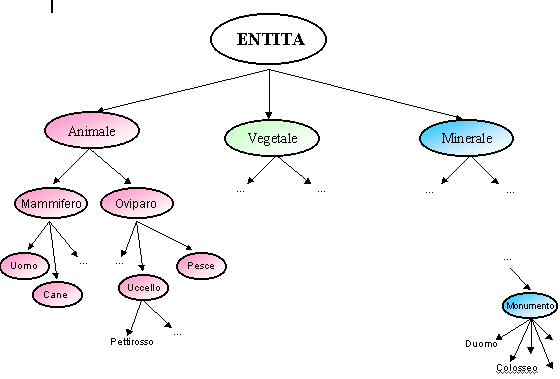
Fig.5.1: Model of the world.
Therefore we define a series of boolean predicate (assuming
that all what it is not explicitly marked as True is False):
Now we can ask to our intelligent agent, equipped of the
world model, a question of the type:
The agent through some simple auto-generated rules of derivations
working on its world model should answer correctly. Using a boolean logic
True/False, the rule of derivation, expressed in a recursive form,
generated to solve the problem "Do the birds moves?" would be
the following:
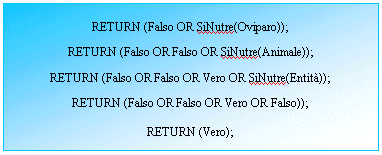
Fig.5.2: Derivation of the rule.
What we did is to verify if the birds derive from one
class X, where X is a class so that ItMoves(X)=True exists.
In such case, according to what we said
previously on the heredity, we can conclude
ItMoves(Birds)=True too.
...and know? Well, you probably remember we were dealing the problem of the
ambiguity and the techniques of disambiguation. Look at the following sentence which
should sound you familiar:
Two meant for the same phrase are too many. It is necessary
to discard one of them. The world representation comes in aid of the
agent. The agent analyzing his world model will deduce (between the other
rules):
Which returns False, indicating to the agent that the
tree cannot perform the action of moving; consequently the second interpretation is
wrong and it can be discarded.
There would be still many things to say about the world model
implementation strategies, but I prefer not to be boring. Last observation: to create
a representation of the world is not sure an easy work, and the
problem is not the huge amount of data needed (which could be solved by
automatic-learning techniques), but their organization, that is the
type of model to adopt. The one I have proposed, is based on object and
heredity, but it is not the only existing strategy (even if perhaps one
of simplest to implement).
The Probabilistic Context Free Grammar (PCFG).
One of the crucial points to deal with in the implementation of
an intelligent agent which can understand the natural language
is choosing the grammar. I'm not going to talk about it in an accurate way.
We just say that an intelligent agent can be equipped with several
different types of grammars, some of simple implementation, others a little more
complex. Obviously, those that work better are the most complex
ones (always supposing they have been written in correct way). We
need to have a fundamental distinguish between in grammars which are independent from
the context (context free), and the grammars which are not independent from the context.
The context free grammars are easier to define through rules just like the following:
Ours agent, equipped with a context free grammar, would
find itself of forehead to the problem to attribute meant to the word
"diamond". The diamond is a precious stone and the name of
the baseball game field. Obvious this is the case the
corrected meant is the second one, but that is deduced from the
context in which " diamond " is inserted. A context free grammar
analyzes the words one to the time, without considering the mean of the previous/successive words and sentences.
To the contrary one grammatical employee from the context would analyze the word "
diamond ", in function of the other words in the phrase (like "
mace ", " ball ", " blow ") and it would probably get to the
correct interpretation.
Someone has tried to solve this type of ambiguities
extending the context free grammars through the introduction of a
parameter which ties, to each production, the probability with which it
is used. Such probability is not constant, but it varies according
to the context of the sentence, to the type of the speaker, and so on.
This new type of grammar takes the name of probabilistic context free
grammar (PCFG). Using a PCFG, the probability that one determined
interpretation is chosen is given from the product of the
probabilities of all the rules that have been used to reach that particular interpretation. Bringing back
here of under the grammar of the extended previous figure with the
probabilistic parameters.